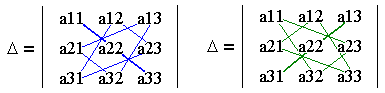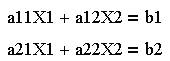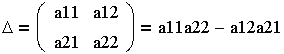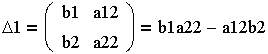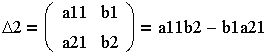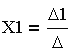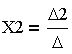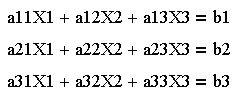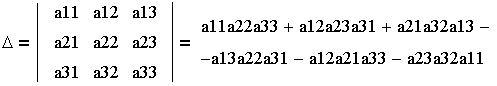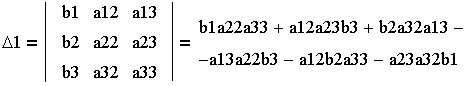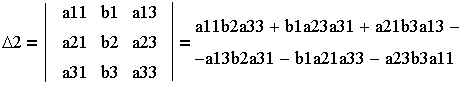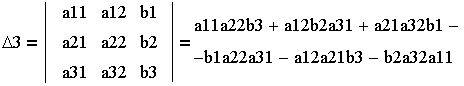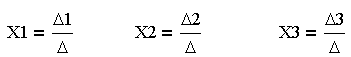§ 3.5. Решение системы линейных уравнений
Решение системы уравнений первой степени с двумя неизвестными через определители
| 1. Исходная система уравнений
|
2. Определитель системы
|
| 3. Определитель для Х1 (заменить первый
столбец определителя системы на свободные члены)
|
4. Определитель для Х2 (заменить второй
столбец определителя системы на свободные члены)
|
| 5. Значение неизвестного Х1
|
6. Значение неизвестного Х2
|
Решение системы уравнений первой степени с тремя неизвестными через определители
| 1. Исходная система
уравнений
|
| 2. Определитель системы
|
| 3. Определитель для Х1
(заменить первый столбец определителя системы на
свободные члены)
|
| 4. Определитель для Х2
(заменить второй столбец определителя системы на
свободные члены)
|
| 5. Определитель для Х3
(заменить третий столбец определителя системы на
свободные члены)
|
| 6. Значения неизвестных Х1, Х2, 3
|
Мнемоническое правило вычисления определителя третьего порядка
Сложить произведения элементов матрицы,
расположенные на главной диагонали (а11а22а33)
и на треугольниках, одна из сторон которых
параллельна главной диагонали (а12а23а31, а21а32а13),
вычесть произведения элементов матрицы,
расположенные на второй диагонали (а13а22а31)
и на треугольниках, одна из сторон которых
параллельна второй диагонали (а12а21а33,
а23а32а11).
D = а11а22а33 + а12а23а31 + а21а32а13 - а13а22а31 - а12а21а33 - а23а32а11