§ 3.4. Метод эквивалентного преобразования схем
Во всех случаях преобразования замена одних схем другими не должна привести к изменению токов или напряжений на участках цепи, не подвергшихся преобразованию.
Замена последовательно соединенных сопротивлений одним эквивалентным. Сопротивления соединены последовательно, если они обтекаются одним и тем же током (рис. 3.4.1)
Рис. 3.4.1 Последовательное соединение сопротивлений
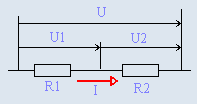
Эквивалентное сопротивление цепи, состоящей из n последовательных сопротивлений, равно сумме этих сопротивлений
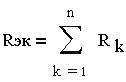 (3.4.1.)
(3.4.1.)
При последовательном соединении n сопротивлений напряжения на них распределяются прямо пропорционально этим сопротивлениям
![]() .
(3.4.2.)
.
(3.4.2.)
В частном случае двух последовательно соединенных сопротивлений
|
|
|
где U — общее напряжение, действующее на участке цепи, содержащем два сопротивления R1 и R2.
Замена параллельно соединенных сопротивлений одним эквивалентным. Сопротивления соединены параллельно, если все они присоединены к одной паре узлов.
Рис. 3.4.2 Параллельное соединение сопротивлений
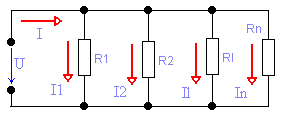
Эквивалентное сопротивление цепи, состоящей из n
параллельно соединенных сопротивлений
(рис. 3.4.2)
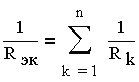
(3.4.6.) или |
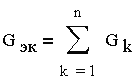 (3.4.7.) |
В частном случае параллельного соединения двух сопротивлений R1 и R2 эквивалентное сопротивление
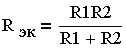 (3.4.8.)
(3.4.8.)
При параллельном соединении n сопротивлений токи в них распределяются обратно пропорционально их сопротивлениям или прямо пропорционально их проводимостям
![]() (3.4.9.)
(3.4.9.)
Ток Is в каждой из них вычисляется через ток I в неразветвленой части цепи
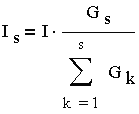 (3.4.10.)
(3.4.10.)
В частном случае двх параллельных ветвей (рис. 3.4.3)
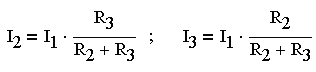 (3.4.11.)
(3.4.11.)
или
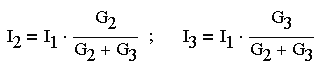 (3.4.12.)
(3.4.12.)
Рис. 3.4.3 Смешанное соединение сопротивлений
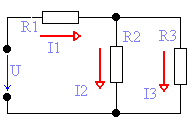 Замена смешанного соединения
сопротивлений одним эквивалентным.
Смешанное соединение — это
сочетание последовательного и параллельного
соединений сопротивлений. Например
сопротивления R1, R2 и R3 (рис.3.4.3.) соединены
смешанно. Их эквивалентное сопротивление
Замена смешанного соединения
сопротивлений одним эквивалентным.
Смешанное соединение — это
сочетание последовательного и параллельного
соединений сопротивлений. Например
сопротивления R1, R2 и R3 (рис.3.4.3.) соединены
смешанно. Их эквивалентное сопротивление
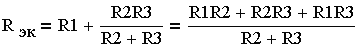 (3.4.13.)
(3.4.13.)
Формулы преобразования треугольника сопротивлений в эквивалентную звезду сопротивлений и наоборот.
Рис. 3.4.4 Треугольник и звезда сопротивлений
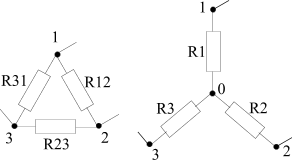
| "Треугольник" > "Звезда" |
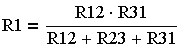 (3.4.14.)
(3.4.14.) |
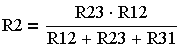 (3.4.15.)
(3.4.15.) |
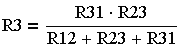 (3.4.16.)
(3.4.16.)
|
| "Звезда" > "Треугольник" через проводимости | "Звезда" > "Треугольник" через сопротивления |
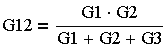 (3.4.17.)
(3.4.17.) |
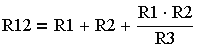 (3.4.20.)
(3.4.20.) |
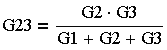 (3.4.18.)
(3.4.18.) |
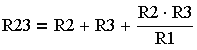 (3.4.21.)
(3.4.21.) |
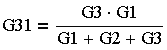 (3.4.19.)
(3.4.19.) |
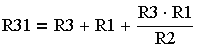 (3.4.22.)
(3.4.22.) |
где G — проводимость соответствующей ветви.
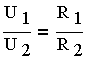 ; (3.4.3.)
; (3.4.3.)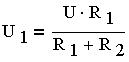 ; (3.4.4.)
; (3.4.4.)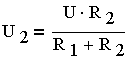 . (3.4.5.)
. (3.4.5.)