§ 2.6. Законы Кирхгофа
|
КИРХГОФ
Густав Роберт Труды по механике, математике, физике. |
В 1847 г. установил законы для электрических цепей, названные его именем. Первый
закон Кирхгофа устанавливает
зависимость между токами для узлов
электрической цепи, электрической цепи, равна нулю
При этом токи,
направленные к узлу, берут с одним знаком
(например, положительным),
|
|
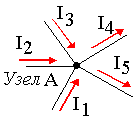
| Рис. 2.6.1. Распределение токов в узле электрической цепи
|
Уравнение по первому закону Кирхгофа для узла А
Преобразуя это уравнение, получим, что сумма токов, направленных к узлу электрической цепи, равна сумме токов, направленных от этого узла
|
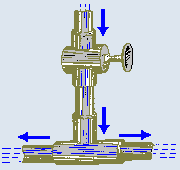
| Для электрического тока
имеет место полная аналогия с распределением потоков воды в соединенных друг с другом трубопроводах. |
Рис. 2.6.2. Распределение
потоков воды в узле трубопроводов
|
| Второй закон Кирхгофа
устанавливает зависимость между ЭДС и
напряжением в замкнутой в замкнутом
контуре электрической цепи алгебраическая сумма
ЭДС равна
При составлении формул,
характеризующих второй закон Кирхгофа, значения
ЭДС Е и падений |
|
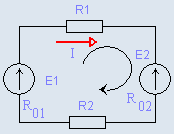
| Рис. 2.6.3. Схема
неразветвленной цепи со встречным включением ЭДС
|
Рассмотрим в качестве
примера электрическую цепь, в которой имеются два источника с электродвижущими силами E1 и E2 (рис. 2.6.3.), внутренними сопротивлениями Ro1, Ro2 и два приемника с сопротивлениями R1 и R2. Применяя второй закон Кирхгофа для этой цепи и выбирая направление ее обхода по часовой стрелке, получим
|
| При этом ЭДС E1 и ток I совпадают с выбранным направлением
обхода контура и считаются положительными, а ЭДС E2, противоположная этому направлению, считается отрицательной. Если в электрической
цепи ЭДС источников электрической энергии при
обходе соответствующего
Встречное направление ЭДС имеет место,
например, на электроподвижном составе при
включении
|
|
| Рис. 2.6.4. Схема
неразветвленной цепи с согласным включением ЭДС
|
Если же ЭДС источников электрической энергии
имеют по контуру одинаковое направление (рис. 2.6.4.), то такое включение называют согласным и ток
В некоторых случаях
такое включение недопустимо, |
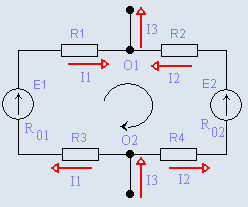
| Рис. 2.6.5. Схема разветвленной цепи
|
Если в электрической цепи имеются ответвления (рис. 2.6.5.), то по отдельным ее участкам проходят различные токи I1 и I2. При составлении уравнения по второму закону
Кирхгофа |
|
|

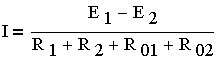 .
(2.6.6.)
.
(2.6.6.)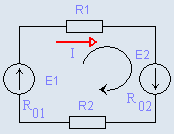
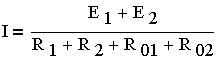 . (2.6.7.)
. (2.6.7.)